W przypadku konstrukcji o podwyższonej odporności na włamanie, statyka montażu to znalezienie odpowiedzi na pytania: jakich elementów montażowych użyć oraz ile ma ich być, aby spełnić wymagania konstrukcji, z zachowaniem odpowiedniego bezpieczeństwa. Sama statyka, jako część mechaniki, zajmuje się obliczeniami oddziaływań na konstrukcję, niezmiennymi w czasie.
Zamontowana w ścianie konstrukcja o podwyższonej odporności na włamanie (POW) musi chronić nas przed atakiem z zewnątrz. Poziom ochrony zależy oczywiście od klasy odporności. W artykule skupiliśmy się wyłącznie na klasach RC2 i RC3. Nie analizujemy też samej konstrukcji POW, a jedynie to, jak musi zostać zamontowana w murze, aby spełniła te wymagania. We wcześniejszych artykułach dot. cyklu montażu przedstawiono różnice pomiędzy konstrukcjami standardowymi (STD) a POW. Omawiany przykład dotyczy jednoskrzydłowej konstrukcji rozwiernej.
Ciężar konstrukcji okna
Główną i jedyną różnicą od strony statyki, pomiędzy konstrukcją POW, a STD jest jej ciężar, czyli stałe obciążenie wewnętrzne. Poniżej przedstawiono różnice w ciężarze pomiędzy oboma rozwiązaniami w klasach RC2 i RC3 na przykładzie dwóch konstrukcji.
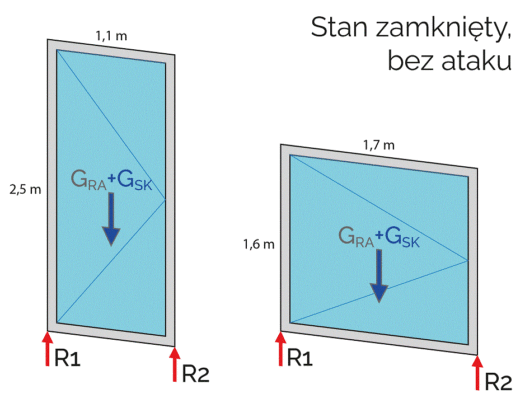
Pierwsza jest pionowa, o wymiarach 1,1 × 2,5 m, druga pozioma, o wymiarach 1,7 × 1,6 m (rysunek 1). Odpowiada to dzisiejszym trendom na rynku (duże przeszklenia) oraz możliwościom technologicznym okuć, które przenoszą ciężar skrzydeł wynoszący do 130 kg. Powierzchnia każdej konstrukcji wynosi ok. 2,7 m2. Z racji wielkości pakietów szybowych w obliczeniach uwzględniono szyby o grubości 4 mm.
Tabela 1:
| 1,1 × 2,5 m | 1,7 × 1,6 m | ||||||
GRA | GSK | G | R1=R2 | GRA | GSK | G | R1=R2 | |
STD | 191 | 787 | 978 | 489 | 175 | 779 | 954 | 477 |
RC2 | 1019 | 1210 | 605 | 1015 | 1190 | 595 | ||
RC3 | 1035 | 1226 | 613 | 1034 | 1206 | 603 | ||
W tabeli 1 w przedstawiono różnice w ciężarze (G) konstrukcji STD, RC2 i RC3 dla obu przypadków oraz wartości reakcji (R) w punktach podparcia. Analiza pokazuje, że większa o ok. 30 proc. jest waga konstrukcji RC2 i RC3, wynikająca przede wszystkim z cięższych pakietów szybowych. Reakcje w punktach podparcia konstrukcji w obu narożnikach R1 oraz R2 są takie same i każda z nich ma wartość połowy ciężaru konstrukcji, czyli R1 = R2 = G/2.
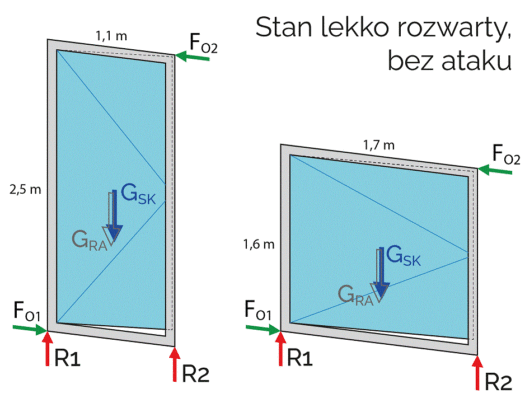
Całkowite zachwianie tego idealnie symetrycznego układu następuje w momencie minimalnego rozwarcia skrzydła (rysunek 2). Pojawiają się wówczas reakcje FO1 i FO2 i zmianie ulegają reakcje w punktach podparcia R1 i R2. Układ taki ma miejsce do momentu pełnego rozwarcia skrzydła (rysunek 3).
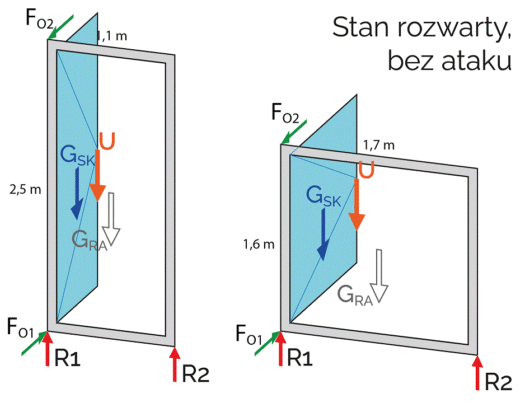
Różnica między stanami przedstawionymi na rysunku 2 i 3 polega na tym, że reakcja FO1 podąża za płaszczyzną skrzydła, natomiast FO2 oprócz podążania za płaszczyzną skrzydła zmienia w sumie punkt przyłożenia. Na rysunku 2 jest w punkcie naprzeciwko zawiasu górnego, na rysunku 3 w punkcie zawiasu górnego. Reakcje FO1 i FO2 co do wartości i kierunku działania są takie same, ale ich zwroty są przeciwne. Wartości tych reakcji zapisano w tabeli 2.
| 1,1 × 2,5 m | 1,7 × 1,6 m | ||||
R1 | R2 | FO1=FO2 | R1 | R2 | FO1=FO2 | |
STD | 1682 | 96 | 525 | 1666 | 87 | 1264 |
RC2 | 1914 | 576 | 1902 | 1390 | ||
RC3 | 1930 | 580 | 1920 | 1398 | ||
Analiza danych z tabeli 2 pokazuje, że ciężar konstrukcji, a w szczególności skrzydła (GSK), w którym zawiera się waga pakietu szybowego, ma znaczny wpływ na reakcje FO1 i FO2. Różnice te wynikają z geometrii konstrukcji. Im większy stosunek b/h, tym różnice są większe. W przypadku b/h = 1,1 / 2,5 = 0,44 wartości reakcji FO1 i FO2 wynosiły ok. 580 N, a w przypadku b/h = 1,7 / 1,6 = 1,06 – ok. 1400 N – przy takim samym ciężarze skrzydła.
Podsumowanie. Większy ciężar konstrukcji POW, w klasach RC2 lub RC3, w stosunku do STD powoduje zwiększenie wartości reakcji w punktach podparcia (R1 i R2) oraz w punktach mocujących przy zawiasach (FO1 i FO2). Zmiany te są proporcjonalne do ciężaru skrzydła (pakietu szybowego) i stosunku wymiarów b/h. Nikłe różnice między FO1 i FO2 nie są jednak podstawą do szczególnego rozpatrywania statyki montażu w przypadku konstrukcji POW. Podobne zmiany są również w przypadku zastosowania pakietów szybowych spełniających wymagania bezpieczeństwa w klasie 1B1, czy też 2B2. Pamiętać jednak należy, że im większy stosunek b/h, tym zmiany mają większe znaczenie.
Obciążenia konstrukcji POW, wynikające z EN 1627
Oczywiste jest, że rozpatrywanie statyki montażu konstrukcji POW dotyczy konstrukcji w stanie zamkniętym (rysunek 1). Norma EN 1627 przewiduje w takim przypadku trzy rodzaje obciążeń, którym musi sprostać konstrukcja POW, są to:
– obciążenia mechaniczne wg EN 1628;
– obciążenia dynamiczne wg EN 1629;
– próba włamania ręcznego wg EN 1630.
Obciążenia mechaniczne wg EN 1628
Według założeń EN 1628, załącznik A.45, omawiany przykład konstrukcji jednoskrzydłowej rozwiernej, musi sprostać sile parcia F3 przykładanej na profil skrzydła w każdym jej narożniku oraz w miejscach zaczepów. Siła ta przykładana jest w każde z tych miejsc osobno, w ustalonej kolejności. Przykład dotyczący wyłącznie dolnego ramiaka ościeżnicy (ze względu na przejrzystość rysunku) przedstawiono na rysunku 4.
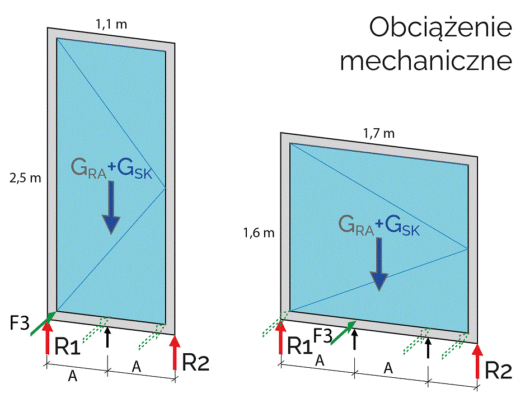
Siła F3 wpływa bezpośrednio na dobór elementu mocującego konstrukcję do muru. Wartość siły F3 w przypadku konstrukcji POW w klasie RC2 wynosi 3kN, w przypadku RC3 – 6kN.
Obciążenia dynamiczne wg EN 1629
Obciążenia dynamiczne, odzwierciedlają działanie na konstrukcję poprzez staranowanie jej całym ciałem. Przede wszystkim sprawdzają „niewypadalność” wypełnienia z konstrukcji skrzydła. Tym samym oddziałują na elementy mocujące konstrukcję do muru. Wydaje się, że wartość tych obciążeń przeniesiona na warunki statyczne powinna być zbliżona do wartości sił F3. W związku z tym postanowiliśmy nie brać ich dalej pod uwagę.
Próba włamania ręcznego wg EN 1630
Głównymi narzędziami stosowanymi przy forsowaniu konstrukcji w przypadku klasy odporności RC2 jest śrubokręt o długości nominalnej 365 mm, a w przypadku RC3 łom o długości nominalnej 700 mm. Ogólny schemat działania tych narzędzi na konstrukcję, a dokładnie na jej ramę (ościeżnicę) przedstawiono na rysunku 5.
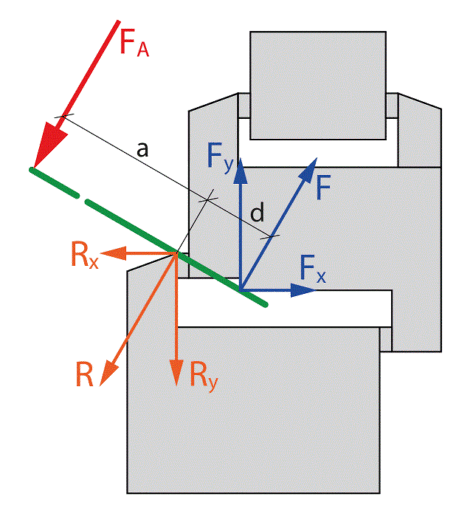
Do obliczeń przyjęto szacunkowo: siłę działania podczas ataku FA = 600 N, odległość d = 30 mm oraz kąt nachylenia śrubokręta/łomu do poziomu równy 30°. Wyliczenia sił zestawiono w tabeli 3.
| FA [N] | L [m] | a [m] | d [m] | R [kN] | Ry [kN] | Rx [kN] | F [kN] | Fy [kN] | Fx [kN] |
RC2 | 600 | 0,365 | 0,335 | 0,030 | 7,3 | 6,3 | 3,6 | 6,7 | 5,8 | 3,4 |
RC3 | 0,700 | 0,670 | 14,0 | 12,1 | 7,0 | 13,4 | 11,6 | 6,7 |
Z przyjętych założeń normowych wynika, że pod każdym zaczepem przymocowanym do ramy (ościeżnicy) musi być punkt mocujący oraz element o określonej ściśliwości, ograniczający znacznie ugięcie ramy (ościeżnicy) pod wpływem składowej siły ataku (Ry). Siła ta może zostać przyłożona w wielu, losowo wybranych miejscach, jednakże dwa z nich są najbardziej niekorzystne. Pierwsze to bezpośrednie oddziaływanie Ry na zaczep, drugie to oddziaływanie Ry w połowie odległości A między punktami mocującymi (rysunek 4). Siła Ry przyłożona w miejscu zaczepu wpływa bezpośrednio na dobór elementu mocującego konstrukcję do muru. Natomiast siła Ry przyłożona w połowie odległości A między punktami mocującymi decyduje o gęstości rozmieszczenia elementów mocujących konstrukcję POW do muru – poza tymi, które znajdują się przy zaczepach. Odległość A nie może być większa niż określona wzorem
A=∛((f_max×48×EJ)/R_y )
gdzie:
A – maksymalna odległość między punktami mocowania [m];
fmax – maksymalne dopuszczalne ugięcie ramy (ościeżnicy) między punktami mocowania [m];
EJ – sztywność przekroju ramy (ościeżnicy) [Nm2];
Ry – siła [N].
Podsumowanie. Przedstawione wyliczenia służą do celów prezentacyjnych i muszą być wykonane dla każdej konstrukcji oddzielnie. Celem było jednak pokazanie mechanizmu i wartości sił, które poprzez mechanizmy dźwigni przekładają siłę wynikającą z ataku FA = 0,6 kN na siłę, w przypadku RC3, działająca na ramę (ościeżnicę) Ry = 12,1 kN, czyli zwiększają ją ponad dwudziestokrotnie.
Obciążenia elementów mocujących
Przenosząc obciążenia mechaniczne i „ręczne” na punkt mocujący, możemy przejść bezpośrednio do wyznaczenia sił działających na element mocujący konstrukcję POW do muru. Wcześniej jednak powinno się pomnożyć wartości sił F3 i Ry przez współczynnik bezpieczeństwa xf. Wówczas otrzymamy siły (rysunek 6)
Ky = Ry × xf [N] oraz Kx = F3 × xf [N]
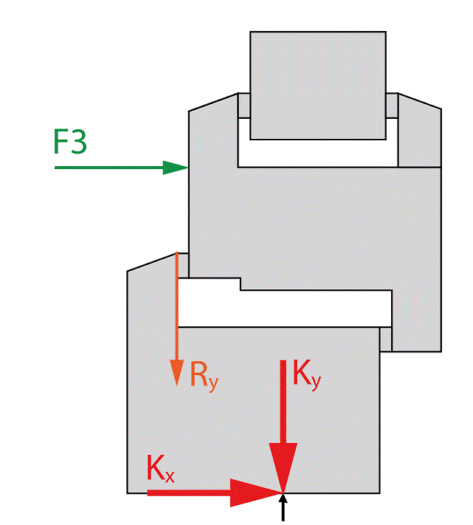
Znając wartości sił Kx i Ky można przejść do etapu związanego bezpośrednio z doborem elementów mocujących konstrukcję POW do muru.
Montaż okna w murze lub w jego licu
W tym przypadku obciążenie od siły Ky przejmie bezpośrednio mur. Należy jednak pamiętać, że w przypadku montażu w licu, w szczególności przy zastosowaniu materiałów ceramicznych, mogą wystąpić zbyt duże obciążenia, które mogą być przeniesione przez krawędź muru. Montaż w licu wymaga również zwrócenia uwagi na minimalne odległości elementu złącznego od krawędzi muru. Obciążenie od siły Kx, siły tnące, przenoszą elementy złączne. W zależności od siły dobiera się odpowiednią średnicę elementu złącznego, zwracając uwagę na minimalne odległości od krawędzi muru.
Montaż okna w ramie poza murem.
Sytuacja zbliżona do powyższej z tą różnicą, że siła Ky musi być przeniesiona na mur przez połączenie klejowe ramy z murem.
Montaż okna na konsolach poza murem.
Ten rodzaj montażu wymaga najwięcej uwagi. We wspomnianych wyżej sposobach montażu występowały wyłącznie siły tnące i naciski powierzchniowe. W przypadku montażu na konsolach dochodzą momenty obrotowe. Jeżeli konsole mocowane są wewnątrz wnęki okiennej, momenty te zwielokrotniają punktowe naciski konsoli na krawędzi muru oraz siły wyrywające elementy złączne z muru. Mocowanie konsol/kątowników po zewnętrznej stronie muru jest bardziej korzystne, gdyż w tym przypadku główną rolę odgrywają siły tnące elementy złączne.
Współczynniki bezpieczeństwa
Aby w odpowiedni sposób dobrać elementy mocujące konstrukcję POW do muru, należy pamiętać o zastosowaniu współczynników obliczeniowych γf uwzględniających materiał, z jakiego został wykonany mur. Wartości współczynników γf przedstawiono poniżej:
γf = 1,8 dla betonu;
γf = 2,5 dla materiałów ceramicznych;
γf = 2,0 dla betonu komórkowego;
γf = 1,3 dla drewna.
autor: Grzegorz Kuligowski
STD – konstrukcja w wykonaniu standardowym;
POW – konstrukcja o podwyższonej odporności na włamanie;
RC2 – konstrukcja o odporności na włamanie EN 1627 RC2;
RC3 – konstrukcja o odporności na włamanie EN 1627 RC3;
GRA – ciężar ramy (ościeżnicy) [N];
GSK – ciężar skrzydła [N];
G – ciężar konstrukcji, G = GRA + GSK [N];
R1, R2 – reakcje podpierające konstrukcję [N];
U – obciążenie pionowe, klasa 4 wg EN 13115;
b, h – szerokość i wysokość konstrukcji [m].
